Questões de Matemática - Geometria - Geometria analítica - Ponto
Um provedor de internet instalará um novo transmissor com um alcance máximo de 3 quilômetros. A fim de estudar com mais exatidão esse alcance, o técnico representou o bairro de interesse num plano cartesiano, onde cada unidade equivale a 1 km. O transmissor foi instalado no ponto (-3, 5). As residências I, II, III, IV e V, cujas posições estão indicadas na figura ao lado, assinaram um plano para receber o sinal de internet desse transmissor, mas uma delas ficou fora do seu alcance.

Qual a residência ficou fora do alcance do transmissor?
Uma matriz em duas dimensõesA2 ×2 é uma matriz de rotação quando a multiplicação de um par ordenado V(x, y) na forma de matriz coluna 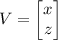 por A produz como resultado um vetor
por A produz como resultado um vetor 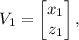 que pode ser identificado com o par ordenado
que pode ser identificado com o par ordenado ) cuja distância à origem é a mesma que V. Nesse contexto, seja a matriz A abaixo, em que a ∈ℝ.
cuja distância à origem é a mesma que V. Nesse contexto, seja a matriz A abaixo, em que a ∈ℝ.
![]()
Considere que a matriz A faça uma rotação por um ângulo α em um ponto P(x, y) do plano, na seguinte forma.
![]()
Então 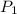 (xcos (α) + ysen(α), - xsen (α) + ycos (α)) é o ponto obtido de pela rotação de P, em torno da origem, por um ângulo α
(xcos (α) + ysen(α), - xsen (α) + ycos (α)) é o ponto obtido de pela rotação de P, em torno da origem, por um ângulo α
Tendo como referência essas informações, julgue o item.
Se α = –π/2, então o ponto ) é rotacionado no sentido anti-horário para o segundo quadrante.
é rotacionado no sentido anti-horário para o segundo quadrante.

Na área da reserva ambiental representada na figura anterior, foi inserido um sistema de coordenadas cartesianas ortogonais xOy, no qual são definidos os pontos A = (-2, 0), B = (–1, 4), C = (2, 3), D = (2, -2) e E = (-2, -2).
Cada ponto (a, b) desse plano cartesiano é identificado com o número complexo z = a + bi, em que a unidade imaginária i é tal que i2 = -1.
Se ZC é o número complexo que representa o ponto C, então (ZC)2 = 5 + 12i.
Analise o gráfico a seguir das funções f, g : ℝ → ℝ e responda a questão.

Sabendo que a área da figura sombreada é dada por h(2) − h(0), onde h(x) = x3/3 + x, assinale a alternativa que apresenta, corretamente, a área da figura hachurada em unidades de área.
As regiões de incidência de certas flores do cerrado foram mapeadas com o auxílio de um sistema de coordenadas cartesianas xOy. A flor caliandra foi encontrada apenas dentro da circunferência de equação x² + y² − 6y + 5 = 0, e a flor flamboyant apenas dentro da elipse esboçada na figura seguinte, na qual também foi traçado o trecho de determinada estrada. Em cada foco da elipse, há uma base de acampamento, e o trecho da estrada está localizado sobre a reta de equação y = −x + 2. As medidas estão em quilômetros.

Tendo como referência as informações precedentes, e considerando 1,41 como valor aproximado da 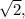 julgue os item.
julgue os item.
A área da região onde foi encontrada a flor caliandra é menor do que a área da região onde foi encontrada a flor flamboyant.
A figura a seguir ilustra um recipiente, no formato parabólico, gerado pela rotação da parábola y = x2 em torno do eixo Oy, para 0 ≤ x ≤ 1 m. O recipiente contém água até a altura de 1/4 m, ou seja, até a abcissa x = 1/2 m.

Para calcular o volume de água no recipiente, será utilizado o princípio de Cavalieri, com o auxílio dos sólidos I, II e III ilustrados a seguir, todos de altura igual a 1/4 m.

O sólido I é formado pela água acumulada no recipiente; o II é igual ao I, porém invertido; o III corresponde a um cilindro reto de raio 1/2 m e altura 1/4 m. Na ilustração, os três sólidos estão alinhados horizontalmente e apresentam dois cortes horizontais, com alturas, em metro, iguais a H e (1/4 – H), para 0 < H < 1/8 m. Dessa forma, como os sólidos I e II possuem simetria vertical, o corte em cinza escuro do sólido I possui a mesma altura do corte em cinza claro do sólido II, e vice-versa.
Considerando as informações precedentes, julgue o item.
A soma das áreas obtidas ao se fazer um corte horizontal nos sólidos I e II a uma mesma altura H independe de H.
Faça seu login GRÁTIS
Minhas Estatísticas Completas
Estude o conteúdo com a Duda
Estude com a Duda
Selecione um conteúdo para aprender mais:





