Questões de Matemática - Álgebra - Cálculo diferencial integral

No século XVII, Kepler descobriu uma fórmula para calcular a área sob o gráfico de uma parábola. Se e são dois pontos no gráfico de uma função do segundo grau , então é possível calcular a área sob o gráfico de , de até , conforme a Figura 1, usando a seguinte fórmula:  onde é o ponto médio do intervalo . Sabendo disso, calcule a área da região hachurada na Figura 2.

 

Com base nas informações dadas, a área da região hachurada na Figura 2 é:

Seja f uma função real, tal que df(x)/dx > 0, ∀x ∈ ℝ, ou seja, a função possui derivada positiva em toda a reta.

 

Portanto, pode-se afirmar que f é uma função:

Considerando a função dada por , julgue o item que se segue.

A função f não está definida em N = 1.

 

    No processo de fazer pipoca, a explosão de cada grão de milho depende, entre outros fatores, da quantidade de água no interior do grão. Quando aquecido o grão de milho, a água no seu interior transforma-se em vapor e, se esse vapor não escapar, intensifica-se, no interior do grão, a pressão sobre seu envoltório, denominado pericarpo. Esse envoltório mantém-se intacto até que a pressão atinja determinado valor que faz que o pericarpo se rompa e o grão exploda. O amido — C₁₂ H₂₀ O₁₀ —, que faz parte da constituição do milho, por ação do vapor de água, também se expande, o que origina a parte esponjosa e branca, que fica exposta.

    Um grão de milho de pipoca é formado pelas seguintes partes: pericarpo, embrião e endosperma, e é composto, principalmente, por amido, água, proteínas, minerais e gordura. A figura acima ilustra detalhes da produção dos gametófitos macho e fêmea e do processo de fertilização do milho. Existem várias linhagens de milho, cujos grãos diferem entre si quanto à forma e à estrutura. Dois parâmetros usados para avaliar a qualidade do milho para pipoca é o tempo que ele leva para se transformar em pipoca e a quantidade de piruás — grãos de milho que não viram pipocas —, em determinado intervalo de tempo de preparo. Considera-se como melhor tipo de milho para pipoca aquele que leva menos tempo para se transformar em pipoca e que gera em menor quantidade de grãos que não viram pipoca.

    Pode-se definir um modelo matemático que permita calcular um parâmetro para se comparar, quantitativamente, diversos tipos de milho. Em termos matemáticos, se m₀ é a massa de milho em quilos que se deseja transformar em pipoca e m(t), a massa de milho em quilos que resta ainda a ser transformada em pipoca no instante de tempo 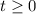, medido em minutos a partir do instante em que, no processo de preparo de pipoca, o primeiro grão de milho estoura, então, um modelo matemático plausível para esse processo estabelece que m(t) = m₀ e^-kt, em que e = 2,7183 é a constante de Euler e k é um parâmetro que pode ser utilizado para determinar a qualidade do milho.

    O valor de k pode ser encontrado experimentalmente, fazendo-se pipocas repetidamente com mesma massa de determinado tipo de milho e calculando-se o valor de k para cada medida. Tirando-se a média aritmética dos valores de k encontrados nas medidas, determina-se o parâmetro q de qualidade do tipo de milho avaliado.

 

A partir das informações do texto e com o auxílio da figura apresentada, julgue o item, considerando que 1 kg de milho de pipoca contenha, no mínimo, 7.500 grãos.

Suponha que, para se determinar o valor do parâmetro q de determinado tipo de milho, 1 kg de grãos tenha sido dividido em 5 partes iguais e utilizado para fazer pipoca, considerando-se, em cada experimento, 10 minutos de preparo, após o estouro do primeiro grão. Se a massa correspondente aos grãos que não estouraram, em cada experimento, foi de respectivamente, 0,02 kg, 0,01 kg, 0,02 kg, 0,04 kg e 0,02 kg, é correto concluir que, para o tipo de milho analisado, .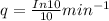

 

    No processo de fazer pipoca, a explosão de cada grão de milho depende, entre outros fatores, da quantidade de água no interior do grão. Quando aquecido o grão de milho, a água no seu interior transforma-se em vapor e, se esse vapor não escapar, intensifica-se, no interior do grão, a pressão sobre seu envoltório, denominado pericarpo. Esse envoltório mantém-se intacto até que a pressão atinja determinado valor que faz que o pericarpo se rompa e o grão exploda. O amido — C₁₂ H₂₀ O₁₀ —, que faz parte da constituição do milho, por ação do vapor de água, também se expande, o que origina a parte esponjosa e branca, que fica exposta.

    Um grão de milho de pipoca é formado pelas seguintes partes: pericarpo, embrião e endosperma, e é composto, principalmente, por amido, água, proteínas, minerais e gordura. A figura acima ilustra detalhes da produção dos gametófitos macho e fêmea e do processo de fertilização do milho. Existem várias linhagens de milho, cujos grãos diferem entre si quanto à forma e à estrutura. Dois parâmetros usados para avaliar a qualidade do milho para pipoca é o tempo que ele leva para se transformar em pipoca e a quantidade de piruás — grãos de milho que não viram pipocas —, em determinado intervalo de tempo de preparo. Considera-se como melhor tipo de milho para pipoca aquele que leva menos tempo para se transformar em pipoca e que gera em menor quantidade de grãos que não viram pipoca.

    Pode-se definir um modelo matemático que permita calcular um parâmetro para se comparar, quantitativamente, diversos tipos de milho. Em termos matemáticos, se m₀ é a massa de milho em quilos que se deseja transformar em pipoca e m(t), a massa de milho em quilos que resta ainda a ser transformada em pipoca no instante de tempo 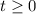, medido em minutos a partir do instante em que, no processo de preparo de pipoca, o primeiro grão de milho estoura, então, um modelo matemático plausível para esse processo estabelece que m(t) = m₀ e^-kt, em que e = 2,7183 é a constante de Euler e k é um parâmetro que pode ser utilizado para determinar a qualidade do milho.

    O valor de k pode ser encontrado experimentalmente, fazendo-se pipocas repetidamente com mesma massa de determinado tipo de milho e calculando-se o valor de k para cada medida. Tirando-se a média aritmética dos valores de k encontrados nas medidas, determina-se o parâmetro q de qualidade do tipo de milho avaliado.

 

A partir das informações do texto e com o auxílio da figura apresentada, julgue o item, considerando que 1 kg de milho de pipoca contenha, no mínimo, 7.500 grãos.

Considere que, em uma lanchonete de cinema, a pipoca seja feita com milho com constante 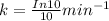 e vendida em sacos com formato de paralelepípedo de dimensões 6 cm × 10 cm × 15 cm. Considere, ainda, que o empregado da lanchonete ponha o milho na pipoqueira e, após 10 minutos do estouro do primeiro grão, ele separe a pipoca do piruá. Considerando-se que o volume aproximado de cada grão de milho seja igual a 0,1 cm³ e que a densidade da pipoca seja 10% da densidade do grão de milho, mantendo-se a massa original, é correto concluir que, com 1 kg de milho, essa lanchonete consegue encher completamente 7 sacos de pipoca, podendo, ainda, sobrar alguns grãos de pipoca na pipoqueira.

A temperatura em uma sala permanecia inalterada até que um aparelho condicionador de ar foi acionado, fazendo com que a temperatura, nesse ambiente, passasse a ser modelada pela função  tal que , sendo  medido em  e , em minutos.

 

Sejam:

 

• a temperatura na sala quando o aparelho foi ligado;

•  o valor para o qual a temperatura nessa sala converge se o condicionador não for mais desligado.

 

Os valores de  e  são, respectivamente, iguais a